Small to Large(큰거 작은거)

# Small to Large란?

Small to Large(큰작(큰거 작은거)이라고도 부름)는 두 집합을 하나로 합치는 것을 반복적으로 할 때 시간복잡도를 줄이기 위해 쓸 수 있는 방법이다.

 

나이브하게 합쳐보자.

두 집합 A, B를 합치려고 할 때, B의 원소들을 A로 옮겨서 합친다고 하면 옮기는 데 걸리는 시간은 B의 크기가 된다.

하지만 이 방법의 worst case를 생각해보면 이는 매우 오래 걸린다.

B의 크기는 x이고 A는 1이라고 해보자. 그러면 x번 옮긴 후 A의 크기는 x+1이 되었다.

그런데 이 다음에는 크기가 1인 집합 C와 A를 합치라고 한다. C에 A를 옮기면 x+1번을 또 옮기게 된다...

따라서 원소의 개수가 n이라고 하면, 전제 원소를 다 합칠 때 최악의 경우에는 n(n - 1) / 2번 옮기는 연산을 해야된다.

 

우리는 저 과정에서 한가지 의문을 품을 수 있다. 왜 큰걸 작은쪽으로 옮기지? 더 작은 집합을 옮기면 더 빠를거 아냐..

그게 small to large다. 저렇게만 해도 시간복잡도가 O(n lg n)으로 떨어진다.

---

# 증명

어떤 두 집합을 합치는 상황을 생각해보자.

크기가 더 작은 집합의 원소들을 더 큰 집합으로 이동시키게(합치게) 되는데, 이 때 작은 집합의 입장에서 보면 합쳐진 후에 집합의 크기는 최소 2배 증가한다.

따라서 각 원소의 입장에서 생각해보면 다른 집합으로 이동하는 횟수는 lg n을 넘지 못한다. (n: 전체 원소 수)

각 원소마다 lg n이하의 이동만으로 전체 원소를 합칠 수 있으므로 전체 시간복잡도는 O(n lg n)이 된다.

 

직관적으로, worst case를 생각해 볼 수도 있다.

어떤 두 집합을 합쳐서 하나의 집합으로 만들 때 필요한 시간은 두 집합 중 더 크기가 작은 집합의 크기만큼이다.

따라서 합쳐진 후의 집합의 크기의 절반 이내에 merge 연산이 수행된다. 

모든 집합이 합쳐진 상태에서 역연산한다고 생각해보자.

worst case에 전체 집합은 그 집합의 크기의 절반인 두 집합으로 쪼개지는 것이고, 이 다음은 재귀적으로 반복된다.

merge sort의 시간복잡도가 O(n lg n)인 것을 보일 때 생각하는 그림과 같은 상황이 된다.

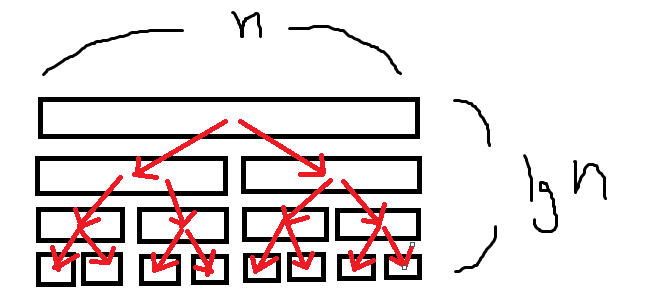
따라서 전체 시간복잡도는 O(n lg n)이 된다.

---

# Small to Large 사용 예시

유니언 파인드를 할 때 rank를 이용해 그룹을 합치는 방법이 있는데, 이것도 small to large가 사용된 예라고 볼 수 있다.

rank는 트리의 높이라고 생각해주면 된다. 정점 하나만 있는 트리의 rank는 1이라고 정의하자.

유니언 파인드를 할 때 자신과 자신의 부모를 잇는 간선들을 생각해주면 각 그룹은 하나의 트리로 나타낼 수 있다.

그룹을 합쳐줄 때 트리의 rank가 더 작은 것을 더 큰 것의 sub tree로 만들어보자. 즉, rank가 더 큰 트리의 루트의 자식노드에 rank가 더 작은 트리의 루트를 추가해보자.

만약 두 그룹의 rank가 같았으면 트리의 rank는 1 증가하게 된다.

만약 두 그룹의 rank가 1이라도 차이났다면 합쳐진 트리는 합치기 전의 트리 중에 더 rank가 큰 것과 같은 rank를 갖게 된다.

rank가 같았을 때에만 rank가 1씩 증가하는데, rank가 x인 트리의 최소 노드 개수를 f(x)라고 정의한다면 rank가 x+1인 트리가 생성되기 위해서는 최소 2*f(x)개의 노드가 필요하게 된다. 즉, rank가 1 증가할 때마다 그 트리의 노드의 개수는 최소 2배 증가한다.

따라서 전체 노드가 n개였다면, 모든 노드를 합쳤을 때의 트리의 rank는 최대 lg n이 되도록 관리할 수 있는 것이다. (이러면 당연히 트리의 루트를 찾는 과정이 O(lg n)에 수행되므로 유니언 파인드의 find 부분이 O(lg n)에 수행되고, union 부분은 rank에 따라 부모-자식 관계 만들어주고 필요하다면 rank를 1 증가시키는 것밖에 안하기 때문에 O(1)에 수행된다. 따라서 rank를 이용한 유니언 파인드는 O(lg n)에 돈다.)